1. From a 1951 issue of The Bent of Tau Beta Pi
|
During the night, snow began to fall at a constant rate. Sometime later, the highway crew
began removing snow from the roads with their one plow. The rate of snow removal (by volume)
was constant, and the plow moved two miles in the first hour and one mile in the second hour.
How long had it been snowing before the crew started?
|

|
2. Adapted from The Chicken from Minsk by Yuri Chernyak
& Robert Rose by Martin Gardner
|
One day two mathematicians, Igor and Pavel, meet in the street.
"How are you? How are your sons?" asks Igor. "You have three sons as I remember, don't you? But
I have forgotten their ages."
"Yes, I do have three sons," replies Pavel. "The product of their ages is
equal to 36." Looking around and then pointing to a nearby house, Pavel says,
"The sum of their ages is equal to the number of windows in that house."
Igor thinks for a minute and then responds, "Listen, Pavel, I cannot find
the ages of your sons."
"Oh, I am very sorry", says Pavel; "I forgot to tell you that my oldest son
has red hair."
Now Igor is able to find the ages of the brothers. What are their ages?
|
3.Adapted from a problem by Rob van Gassel, Jurgen Heijmans and Edwin van Veldhovenvia,
from The Ultimate Puzzle Site
|

|
This b-day cake must be cut into eight equally-sized pieces. Cuts must be perfectly
straight, however. Explain how to cut the cake into eight pieces with exactly 3 straight
cuts.
|
4. Adapted from a problem by Ken Rosato via Technology Review
|
Two climbers who specialize in climbing square-based Egyptian-style pyramids intend to
compete by racing to the top of a pyramid which sits on a 250,000 sq. ft. base. One climber
will take the easy route (along one of the corners) while the other plans to climb along the
steepest path, directly up the middle of one of the faces. These two climbers will experience
different angles of ascent. The question: What height pyramid will have the greatest difference
in angles of ascent?
|

|
5. Adapted from Technology Review by Ramon Mireles
|

|
Two trains on parallel tracks pass in the night. One is a 715 ft. freight train and the
other is a 275 ft. passenger train. Approximately an hour after they passed each other
(it took 9 seconds to completely pass) the faster train stopped and then reversed direction.
It overtook the slower train and passed it completely in 45 seconds. How fast were the
two trains going?
|
6. Adapted from An Enigma by Stephen Ainley via The Bent of Tau Beta Pi
|

|
Triangle Town is a city bounded by three straight borders called A, B,
and C. The lengths of these three borders are integer numbers of miles (no fractions)
with all three border lengths different. Curiously, all of the following computations yield
results which are perfect squares: A+B+C, A+B-C, A-B+C, and -A+B+C. If Triangle Town has
the smallest perimeter consistent with the above statements, what is the length of each of
its borders?
|
7. Adapted from a problem by William W. Verkuilen via The Bent of Tau Beta Pi
|
In an alien world of 16-fingered people (eight on each hand), the hexadecimal number system
is used exclusively. Interestingly, their coins are denominated 1, 5, 10, 25 and 50 just like
ours, except that their coins' values are hexadecimal (i.e. their 10-cent coin can be exchanged
for 16 of their 1-cent coins). Furthermore, they love to gamble as evidenced by their toll
bridge, which instead of charging a fixed toll, flashes the toll as a random number from
1 through 100, inclusive, and hexadecimal, of course. To use the exact-change lane, how
many coins of each denomination must a traveler carry in order to have the least total value
of coins and still be able to exactly pay any toll?
|
8. Adapted from a problem by Daryl Cooper via The Bent of Tau Beta Pi
|
What is the minimum number of knights that is required so that every square on a standard
8 x 8 chessboard is either occupied by a knight or else threatened by a knight?
A square is threatened if a knight can move to that square. Recall that a knight moves
two squares forward, back, right, or left, and then one square perpendicular to that
direction, landing on a square opposite in color to its starting point. The move can
occur even if intervening squares are occupied.
|

|
9. Adapted from a problem by Thomas R. Diaz-Davilla via The Bent of Tau Beta Pi
|
An integer N consisting of five non-zero digits, all of which are different, has the
curious property that it is equal to the sum of all the different three-digit permutations of
its five digits. Find N.
|
10. Adapted from Technology Review via The Bent of Tau Beta Pi
|
An urn contains nine balls labeled 1 through 9. Pretend that you draw the balls
from the urn, one at a time, at random, and line them up in the order drawn to form
a nine-digit number. What are the chances (the probability) that the nine-digit number
is divisible by eleven, with zero remainder?
|
11. Adapted from New Scientist
|

|
Prof. Peek is pleased with the new extension telephone number in his office because it has four
digits, the middle two of which are identical. "Like my name", he exclaims! The repeated
digit is also the first digit of his secretary Miss Eagle's new four-digit number.
Moreover, Peek's first digit is the same as the first digit of Dr. Sparrow's new four-digit
number.
If you interchange the first and last digits of Dr. Sparrow's number, you get Miss Eagle's
number. If you subtract Sparrow's number from Eagle's, you get Peek's.
So what is Prof. Peek's new extension phone number?
|
12. Adapted from a problem recently published by H.K.Tay
|
When Poisson, philosopher and mathematician (21 June 1782 to 25 April 1840) was young,
he offered a solution to the following little problem.
You have three bottles. One can hold exactly 12 liters, the second holds 8 liters, and
the third holds 5 liters. The 12 liter jug is filled with water. The objective is to divide
the water in half, one half residing in the 12-liter bottle and the other half residing
in the 8-liter bottle. What is the minimum number of times that he must pour from one
bottle into another to achieve this goal?
|
13. Adapted from IEEE POTENTIALS
|
A Philosophy professor and his favorite student entered a railroad tunnel,
looking for the meaning of life. When they were two-fifths of the way
in, they heard a train coming behind them. The professor, being wiser, made
a quick calculation and then decided to run back toward the entrance, just
barely getting out as the train entered the tunnel. His student chose the
longer way, and he escaped at the opposite end just as the train left the
tunnel. Both prof and student ran at 20 km/hr. How fast was the train going?
|

|
14. Capturing the Queen
|

|
Two men are about to play a game on a chess board using only two pieces. The
first player has a queen, and the second player has a knight. Here is how
the game is played ... Both players close their eyes while the first player
places his queen on the board at random (all positions being equally
likely)and then opens his eyes. It is now the second player's turn, and he
gets two chances to capture the queen in this turn. With his eyes still
closed, he places his knight on the board at random and then opens his
eyes. If the initial placement of his knight did not capture the queen, he
completes his turn by moving his knight (and possibly capturing the queen).
What is the likelihood (expressed as a percentage) that the second player
will capture his opponent's queen?
|
15. An Old Coin-Tossing Game
|
Ostap & Osric like to gamble, not for money but just for the fun of it.
One day, they decide to compete by taking turns tossing a fair 1943
steel penny. The first one to get Heads wins.
What is the likelihood (expressed as a percentage) that the first
man to toss will win? (e.g. 100% chance, 50% chance, etc.)
|
16. Here is a problem that won't steal much "time" from your studies
|
Gary and Vadim shared an apartment in a dormitory building on campus.
One day, G needed a battery for his remote. And so, while Vadim was sleeping,
he took the battery out of their only clock. When Vadim awoke, he quickly discovered
the dastardly deed, and inserted a new battery. Not knowing the correct
time, he looked out the window, estimated the position of the moon in the
sky, and then set their clock to 6:31 PM-VST (Vadim Std Time).
He immediately left the room and walked to visit friends. Upon arriving, he noticed
that the time was exactly 6:33 PM-GMT. He stayed for exactly one hour and
then walked back to his room, arriving there at 8:01 PM-VST. Vadim looked
at his clock, thought about the situation for a second or two, and then
correctly reset it to ___ PM-GMT.
To what time (GMT) did he reset the clock?
|

|
17. Balance-scale problems are classic, dating back thousands of years
|

|
Claudia has 25 diamonds. Twenty four (24) are real, and one is an
imitation. All of them are of equal weight except for the imitation
which is slightly lighter than the real diamonds. If Claudia decides
to use a balance scale to find the imitation, with luck she could find
it with a single weighing (she could randomly select two stones to
weigh, one of which is the imitation). Without luck, it will take her
more than a single weighing. It should NEVER take her more than
N weighings, however. What is the smallest N? _____ Explain.
|
18. Adapted from Wells, THE PENGUIN DICTIONARY OF CURIOUS & INTERESTING NUMBERS
|
The number 3,435 = 3^3 + 4^4 +3^3 + 5^5 where ^ indicates exponentiation.
That is, it is equal to the sum of its digits each raised to that digit's
power. Find the next larger such number. [use the convention 0^0 = 0]
|
19. A Classic Candle Problem
|
You are boiling a chicken in a pot, and you know that it should be boiled
for 45 minutes. Unfortunately, you do not have a clock, and the boiling
has just begun. How can you use two one-hour candles to measure the required
cooking time? You are not allowed to use any measuring devices
(no rulers, no scales, etc.) other than the candles, themselves
|
20. Adapted from Litton Industries, THE BEST OF PROBLEMATICAL RECREATIONS
|
Ursula has 36 cloth napkins. Eleven are red, thirteen orange, five yellow,
two green, and five blue. From this pile, she plans to select and tie
three napkins together, end-to-end. How many essentially-different color
combinations can she create without having two napkins of the same color tied
next to each other?
|
21. Adapted from Oswald Jacoby, MATHEMATICS FOR PLEASURE
|
Buses leave Boston for New York City every hour on the hour, and
return from New York City to Boston every hour on the half-hour.
All buses use the same highway, and the trip takes five hours each way.
As you ride from Boston to NYC, how many returning buses would you pass?
|

|
22. Contributed by JenM of American Mgt. Systems
|
|

|
Below is a quiz attributed to Albert Einstein. It is reported that he
said that 98% of the people in the world cannot solve this problem.
Are you among the other 2%?
Here are the facts:
There are 5 houses in 5 different colors.
In each house lives a person with a different nationality. These 5 owners
drink a certain beverage, smoke a certain brand of cigar and keep a certain
pet. No owners have the same pet, smoke the same brand of cigar or drink
the same drink.
|
Hints:
01: The Brit lives in a red house.
02: The Swede keeps dogs as pets.
03: The Dane drinks tea.
04: The green house is on the left of the white house.
05: The green house owner drinks coffee.
06: The person who smokes Pall Mall rears birds.
07: The owner of the yellow house smokes Dunhill.
08: The man living in the house right in the center drinks milk.
09: The Norwegian lives in the first house.
10: The man who smokes Blend lives next to the one who keeps cats.
11: The man who keeps horses lives next to the man who smokes Dunhill.
12: The owner who smokes Blue Master drinks beer.
13: The German smokes Prince.
14: The Norwegian lives next to the blue house.
15: The man who smokes Blend has a neighbor who drinks water.
The question is ... Who keeps fish? ... What does he drink? ... What does
he smoke? ... In which color house?
23. Adapted from Oswald Jacoby, MATHEMATICS FOR PLEASURE
|
I just returned from shopping at the North Campus Book Store. I was
going to purchase an inexpensive pen, and I found that I could pay for
it using exactly four standard U.S. coins, but not fewer. ILya wanted one
too, and he told me that I could purchase a pair of pens with a minimum of
six coins. Max convinced me to buy one for him, too, by pointing out that
I could purchase three pens with just two coins. What was the price of a pen?
|
24. How old is Bob?
|
Bob submitted answers to last month's Challenge problems with a personal note
attached. He reported that he had reached age N in November of the year
N-square (4-digits). How old is he now?
|
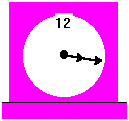
25. A Classic Clock Problem
|
What is the first time after 3 o'clock when the minute hand and the hour
hand of a clock line up ?
|
|
26. Adapted from Oswald Jacoby, MATHEMATICS FOR PLEASURE
|
Professors from PL, ME, CE, CN, and EE Departments and their wives recently
sat together at a large circular table in the main UMASS-Lowell Dining Hall.
The seats were so arranged that the men and women alternated and each woman
was three places distant from her husband. The wife of the CE professor sat
at the right of the Plastics professor. The EE professor sat two places to
the left of the CE professor, and the wife of the EE professor sat two places
to the right of the wife of the ME professor. If the wife of the Plastics professor
looked to her left, who would she have seen sitting next to her?
|
27. Adapted from the Journal of Recreational Mathematics via The Bent of Tau Beta Pi
|
Every Challenge should contain a cryptic. This one is special because it is not
solvable in base-10, despite the wording. Your job is to solve it in the smallest base for
which a solution exists. The usual rules of cryptics apply (e.g. None of the leading digits
are zeros).
TEN x TEN - TEN = NINETY
|
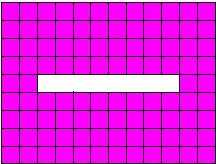
28. Adapted from The Bent of Tau Beta Pi
|
A 9-ft. by 12-ft. rug has a centered rectangular hole which measures 1-ft. by 8-ft
as shown. Show how to cut the rug into two pieces
that can be fit together to form a 10-ft. by 10 ft. rug with no hole.
| |
|
|