|
1. Plowing the Snow
2. Product of Their Ages: First, the problem is meaningful only if all the ages are integers. You must assume that! The next step is to use the 1st condition, that the product of the sons' ages is 36. This allows only 8 possibilities: age1 age2 age3 sum 3. Three straight cuts: 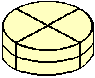
1) Cut the cake in half horizontally. (One cut.) 2) Cut the cake in quarters vertically. (Two cuts.) 3) Serve with lemonade. Sticklers will note that it is technically possible to reverse steps 1 and 2, although I expect it would be somewhat messier. 4. Difference in Angles of Ascent: Height = 300 ft. Assume a square base with sides of length 2. You can draw two right triangles, one with the steep incline as hypoteneuse and a base of one, and the other with a pyramid corner as hypoteneuse and a base of sqrt(2). Both triangles have the same height (the peak of the pyramid). A simple spread sheet reveals that the greatest difference in angle of incline occurs at a height of 1.2. This is a height to square-base side ratio of 0.6. The actual pyramid base measures 250,000 sq. ft. The square base-side length measures 500 ft. Using the ratio 0.6, the height must be 300 ft.
radian radian radian
Hgt Steep ang Corner ang Difference
=== =========== =========== ===========
1 0.1 0.099668652 0.070593179 0.029075473
2 0.2 0.197395560 0.140489702 0.056905858
3 0.3 0.291456794 0.209033299 0.082423495
4 0.4 0.380506377 0.275642799 0.104863578
5 0.5 0.463647609 0.339836909 0.123810700
6 0.6 0.540419500 0.401247142 0.139172358
7 0.7 0.610725964 0.459619331 0.151106633
8 0.8 0.674740942 0.514805955 0.159934987
9 0.9 0.732815102 0.566752326 0.166062776
10 1.0 0.785398163 0.615479709 0.169918455
11 1.1 0.832981267 0.661067893 0.171913374
12 1.2 0.876058051 0.703638951 0.172419099 <<< greatest difference of 9.88 degrees
13 1.3 0.915100701 0.743343175 0.171757526
14 1.4 0.950546841 0.780347572 0.170199268
15 1.5 0.982793723 0.814826916 0.167966807
16 1.6 1.012197011 0.846957073 0.165239939
17 1.7 1.039072260 0.876910263 0.162161996
18 1.8 1.063697822 0.904851874 0.158845948
19 1.9 1.086318398 0.930938456 0.155379942
20 2.0 1.107148718 0.955316618 0.151832100
21 2.1 1.126377117 0.978122560 0.148254557
5. <Two trains in the night: 66 and 44 ft/sec 6. Triangle Town: The three borders measure 26, 80, and 90 miles. 7. Hexadecimal Coins: If you first convert from hexadecimal to decimal notation, the coins in use are 1, 5, 16, 37 and 80-unit coins, and a driver must be able to produce any value up to 256 units. The smallest total value is (hopefully) 256, and we must look for the least number of coins that wil sume to this value and still permit paying any toll. Working backwards, we see that we can use two 80s, one 37, two 16s, four 5s and seven 1s. Thus, a driver must carry 16 hexadecimal coins: seven 1s, four 5s, two 10s, one 25 and two 50s. 8. How many knights?: Twelve knights are required so that every square on a standard chessboard is either occupied or threatened. 9. Five-digit integer: The number 35,964 has the curious property that it is equal to the sum of all the three digit permutations of its five digits. 10. Nine-digit number divisible by 11: The probability is 11/126 or 0.0873 11. Prof Peek's Phone Number: Represent Peek's telephone number by PEEK, Eagle's by EXYP and Sparrow's by PXYE. They have the relationship EXYP - PXYE = PEEK. Inspection shows that E=9 and P=4, requiring that K=5. Thus Prof Peek's number is 4995. 12. Water, water, everywhere: 7 times
13. The Train & the Tunnel: Let x be its dist from the tunnel when the train was first heard; let L be length of the tunnel; let v be velocity of the train. Then x/v is the time it took for the prof to run a distance of two-fifths of L. This must equal 2/5 * L / 20. Similarly, (x+L)/v = 3/5 * L / 20. You work on these two equation and discover that v = 100 km/hr. 14. The King & the Knight: You would probably be wise to deal with only 1/2 of the board which contains 32 positions. Board symmetry guarantees that you will get the same likelihood of capture, regardless of which half of the board the queen lands on. Symmetry also dictates that you can restrict your analysis to just the black since you will get the same likelihood of capture whether the queen lands on black or white. That leave only 16 squares to be checked. Now just total 1/16 times the likelihood of capture for each of the 16. [Note: For any one of the 16, the likelihood of capture is the # of threatening positions on the total board) / 64 ] If you do it right, you get 9.375% for your answer. 15. Tossing the Coin: The answer is that there is a 66.67% chance that the first tosser will eventually win. The solution goes like this: Let's assume that he is going to win. The chances that it will happen on the first toss is 50%, or 0.500 If he didn't win on the first toss, he still has the additional chance to win on the third toss. For that to happen, he has to lose on the first toss, his opponent has to lose on the second toss, and he has to win on the third toss. The chance of that happening is (0.5)(0.5)(0.5) or 0.125 Thus, he has more than just a 50% chance of winning because he gets more chances if he doesn't win on the first toss. Add the two numbers, and you get a total chance of winning of 0.625 (62.5%) if you allow him to win on either the first or third toss. If he didn't win by the third toss, he can still win on the fifth toss. The chance of that happening is (0.5)(0.5)(0.5)(0.5)(0.5) or 0.03125 Add the numbers and observe that he has a 0.65625 (65.625%) chance of winning on the first, third, or fifth toss. Continue in this way, and even without any fancy series algebra you will observe that his TOTAL chance of winning converges rapidly to 66.67% 16. Setting the Clock: 7:48 P.M. EST NOTES (edited from "Notes" submitted by SteveL): 1. The answer to question a is based on the assumption that it took Vadim exactly the same amount of time to walk to the park and from the park. I suppose this is a fairly reasonable assumption, but there is no way to be positive. What if one way was steeply uphill and the other steeply downhill? 2. The answer to question (a) is also based on the assumption that Vadim Standard Time is a system of measuring time that is based on a 60 minute hour. Again, this seems like a very reasonable assumption, but I can't be sure, since I've never heard of this system before, and the challenge, in and of itself, does not give sufficient data to check this assumption. 3. Vadim's recent move from the Boston area to greater London does not have any impact on the answer to part (a). 4. Anyone who lives with G should consider investing in an electric clock. He'd save a lot of money on batteries. 17. Minimum Number of Weighings: 3 weighings. Divide them up in lots of 9,9,7 for 1st weighing The minimum number of weighings that always finds the fake diamond is 3. There is more than one way to find it in 3 trials, however. Here is the worst case:
trial Left-balance Right-balance On the side
1 9 9 7
2 3 3 3
3 1 1 1
18. 438,579,088 19. A Chicken in Every Pot: Light one candle at both ends, and the second candle at only one end. It takes 30 minutes for the first candle to be consumed. Now light the other end of the second candle so that it will burn for an additional 15 minutes. Remove the pot from the heat, and then put it into the refrigerator to cool. Later, skim the fat from the top. Remove the chicken and cut it into cubes. Heat the soup to boiling, add the cubes, one-half cup of rice, one cup of water, one tablespoon of instant chicken soup powder, three tiny peeled onions, and two carrots. Bring it all back to a boil and simmer on low heat for 10 minutes. Serve piping-hot. 20. Ursula's Napkins: First, there are 20 combinations where the first and third napkins have the same color [ 5 color choices for the middle position, and 4 choices for the end-position color] Then there are 5x4x3 or 60 combinations containing 3 colors. But half of these are just mirror images of the other half, and are not "essentially-different" color combinations. So take half of the 60 and add it to the 20 to obtain an answer of 50. 21. The buses: You would pass the first returning bus fifteen minutes after you start (you are 15 minutes out of Boston, and the returning bus is due in Boston 15 minutes later), and one each half-hour thereafter. That's a total of ten. 22. Einstein Quiz: The German keeps fish. He drinks coffee and smokes Prince in a green house. 23. Price of Pens: It costs 17 cents. 17 = 1 + 1 + 5 + 10 34 = 1 + 1 + 1 + 1 + 5 + 25 51 = 1 + 50 24. How old is Bob? Bob turned 44 in the year 1936 That was 62 years ago, making Bob 106 years old. 25. The clock: The minute hand on a clock moves 12 times faster than the hour hand. Starting at time 3:00, the minute hand will move (15+x) while the hour hand moves 1/12 that distance, namely x. And so we begin by writing (15+x)=12x. This yields x=15/11 or 1 3/11. The time: 3:16 3/11 26. Seating arrangement: The CN professor sat on the left of the Plastics professor. The seating arrangement was: CN - pl - ME - cn - EE - me - CE - ee - PL - ce 27. Cryptic: TEN X TEN - TEN = NINETY 674 x 674 - 674 = 404761 28. Cutting the Rug 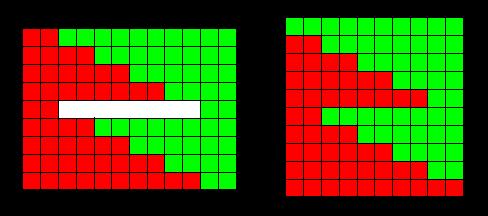
|
